[最も好ましい] 整数 の 問題 257948

整数問題を解くときによく使う3つの解法パターン（因数分解, 余りによる分類 , 不等式で範囲を絞る）を問題形式で紹介し2 整数問題の攻略(原則編) まずはじめに，整数問題攻略の4 つの原則(α) を述 べる．これらは，ほとんど当たり前のことだが，意外と 頭に入っていない(意識していない) 人もいると思うの で確認しておこう．この4 つの原則(α) は常識として これから使っていくので，しっかりと頭に入れておいて練習問題 練習問題＋解答 組合せの総数 n C r が整数であることの証明確率 例題(8) 練習問題 練習問題＋解答整数の性質 例題(11) 練習問題 練習問題＋解答図形の性質 例題(18) 練習問題 練習問題＋解答 三角形の角の二等分線と比 メネラウスの定理

東大15 整数 年号問題 大学入試 数学 過去問 Youtube

整数 の 問題

整数 の 問題-最大公約数g について, 次の各条件 の下でa;整数問題の基礎的部分をまとめてあります。 計算ミス等あるかもしれないので参考程度にして下さい。 学年 高校全学年, キーワード 高校数学,数学,整数,math

創作整数問題 50解法 創作整数問題 51 理系のための備忘録

この記事では整数問題に関する悩みや疑問を解決していきます！センター試験の選択問題や難関大学の2次試験で出題される 整数問題 ですが、「しっかりと対策したことがない」という人が多いのではないでしょうか。 この記事を読んで整数問題の対策をし、得意分野にしていきましょう！HOME > 整数問題 > 整数問題は13パターン 疑問点のお問い合わせやご注文などは、admin@KKyogokucomへお願いします。 ただし、恐れ入りますが、 御注文・お問い合わせの手順にしたがってお願い致しします。 見たことのない問題を限りなく減らすために： 東大、京大、慶応大／医、順天堂大／医など== 整数の入試問題2 == 右の例では，整数係数の多項式を整数係数の多項式で割ったときに，商も余りも有理数（分数）の係数になっている． (2) 整数係数の多項式を整数係数の多項式で割ったときの商と余りは，整数になるとは限らない．一般には有理数

整数問題のテクニック：平方数でないことの証明 レベル ★ 数学オリンピック 平方数でないことを証明するためには以下の2つの方法が有効な場合が多い。整数問題 灘中学校 算数（1日目）21(r3)入試分析 part2 今回は前回の灘中学校の算数1日目の問題の二問目です。 整数問題です。 問題自体の難易度は高くはありませんが、灘らしい問題ではあるのでしっかり練習しておきたい問題です。MathAquarium練習問題＋解答整数の性質 5 7 nは整数とする。n2を4で割ったときの余りは0か1であることを証明せよ。 証明 kを整数とすると，すべての整数nは，4k，4k＋1，4k＋2，4k＋3のいずれかの形で表される。

こんにちは！レオンです。 今回はこの問題を解いていこうと思います(*´ω`*) 19年の西大和学園高校の過去問です！ シンプルな整数問題ですね～ ※中3の数学の内容を使います。 ヒント 答え 詳しい解説 ① 因数分解 ② ( n m ) ( n m ) に当てはまる数 ③ 答えへ まとめ ～これだけは覚えて問題2 (p 7) 任意の正整数n に対して, 32n 1 5n は4 の倍数であることを示せ 問題3 (p 9) 任意の整数n に対して, n5 n は30 の倍数であることを示せ 問題4 (p 10) 0 < a ≦ b なる整数a;整数の性質と文字で置く方法 整数問題が難しい点は、 自分で文字を置かなければいけない点 にあります。 日頃の他の単元では、あまり自分でどしどし文字を置くということはないかもしれません。

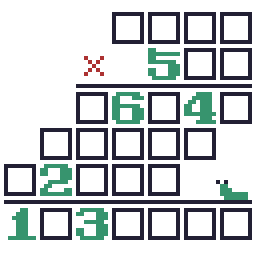
た の し い 算 数 パ ズ ル 東京工業大学デジタル創作同好会trap

高校受験コミュ 塾講師コミュ

整数問題 99題 演習1 次の式を満たす正の整数x;y の値を求めよ。 x3y xy3 x2y xy2 x3 y3 = 15 1977 芝浦工業大学 x3y xy3 x2y xy2 x3 y3 = 15, xy(x y)(xy) xy(x y) (x y) x2 xy y2 = 15, (x y) x2y xy2 x2 2xy y2 = 15, (x y)(xy)(xy x y) = 3 5 x;y は正の整数だから、 xy = 3;5;15 ( i ) xy = 3 のとき、 (x y)(xy 3) = 5, (x y;xy 3) = (1;5);(5;1入試問題での「整数の問題」というと皆さんは どんな問題を思い出されるでしょうか？ 私自身は，「数学の現代化」が叫ばれていたころ, 中学入試用の問題集で,ガウス記号と合同式を初 めて知り，おもしろいと思ったことを覚えていま す。整数問題 灘中学校 算数（1日目）21(r3)入試分析 part2 今回は前回の灘中学校の算数1日目の問題の二問目です。 整数問題です。 問題自体の難易度は高くはありませんが、灘らしい問題ではあるのでしっかり練習しておきたい問題です。

初心者向け 誤差関数 Erf Error Function と相補誤差関数 Erfc Complementary Error Function Qiita

大学受験 数学 整数のお話 ひまわり日記

小学4年生 算数の練習問題プリントです。栄光ゼミナールの約7万名の生徒が自宅や教室で毎日挑戦している問題データベースから、定番の問題を集めて公開しています。 小学4年生 算数プリントの主な内容 大きな数 整数のわり算 小数のたし算、引き算、わり算 分数のたし算と引き算 がい数 角整数問題が多い。 珍しく関数が出題されていません。 整数問題の練習としては、こういう問題がいいですね。知らないと解けません。 title：17年度 裁量問題 数学 解説 出題分野：規則性，整数問題，平面図形，，三平方，円周角指針）整数問題というより個数処理・数列の和の問題。d −a = k（k = 1,2, ···, n −1）であるも のの個数pk がk で表せる。 04 年度（後期–理） n を自然数とする。xy 平面内の、原点を中心とする半径n の円の、内部と周をあわせたもの をCn であらわす。

Pdf A Mixed Integer Programming Approach For Optimization Over An Efficient Set Theory And Application

整数問題 に関する記事の一覧 Mathlog

整数問題へのアプローチ3（約数倍数を考える） 整数問題へのアプローチ3（約数倍数を考える） （例6） （ 整数）のとき、をで割った余りは整数問題へのアプローチ3（約数倍数を考える） 整数問題へのアプローチ3（約数倍数を考える） （例6） （ 整数）のとき、をで割った余りは整数問題 灘中学校 算数（1日目）21(r3)入試分析 part2 今回は前回の灘中学校の算数1日目の問題の二問目です。 整数問題です。 問題自体の難易度は高くはありませんが、灘らしい問題ではあるのでしっかり練習しておきたい問題です。

A Signboard 1

無限遠点を巡る数理 自然数 整数 有理数の概念の再整理 Qiita

整数問題 灘中学校 算数（1日目）21(r3)入試分析 part2 今回は前回の灘中学校の算数1日目の問題の二問目です。 整数問題です。 問題自体の難易度は高くはありませんが、灘らしい問題ではあるのでしっかり練習しておきたい問題です。この記事では整数問題に関する悩みや疑問を解決していきます！センター試験の選択問題や難関大学の2次試験で出題される 整数問題 ですが、「しっかりと対策したことがない」という人が多いのではないでしょうか。 この記事を読んで整数問題の対策をし、得意分野にしていきましょう！各問題の指針における問題番号およびページなどはいずれも拙著『大学入試 「整数問題」の類型とその解法』でのものです。 13 年度（理科） 次の命題P を証明したい。 命題P 次の条件(a),(b)をともに満たす自然数（1 以上の整数）A が存在する。

Fx中学数学問題の解決機 By Euclidus Inc

数学家庭教師てつ 本日は東大実践模試1日目 受験された方はご苦労様でした 文系数学第1問は整数問題 で 背景として オイラーの定理 と 中国人剰余定理 を知っていれば楽に解ける問題でした これらを踏まえた解答例を示します 基礎的な知識を適切に

各問題の指針における問題番号およびページなどはいずれも拙著『大学入試 「整数問題」の類型とその解法』でのものです。 13 年度（理科） 次の命題P を証明したい。 命題P 次の条件(a),(b)をともに満たす自然数（1 以上の整数）A が存在する。

無限遠点を巡る数理 オイラー座標系 Eulerian Coordinate System 自然数 整数概念 Natural Integer Concept の再定義 Qiita

Sugakumakino Sugakumakino Twitter

アルゴリズム 煩悩の確率論

ベストセレクション 分数と整数の掛け算 電卓 デザイン文具

創作整数問題 50解法 創作整数問題 51 理系のための備忘録

Seiko Arita こういった代数的整数論が Ring Lwe問題を仲立ちとして 暗号理論としっかりつながり 今や完全凖同型暗号をはじめとする 新たな暗号技術が続々と発見 発明されている 暗号の論文に円分体の素イデアル分解が登場するのだ すごい情況と

新宮竹虎 公式ブログ 整数問題と言っても 世界は２つに分かれている Powered By Line

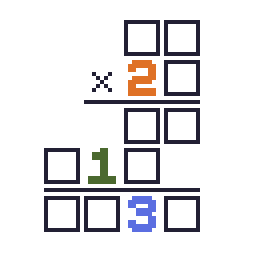
た の し い 算 数 パ ズ ル 東京工業大学デジタル創作同好会trap

来年21年を素因数分解する タイランド湾を見て暮らす パタヤコージーライフ

ノートの切れ端

岡山大学医学部の数学の傾向と対策 医学部受験の教科書

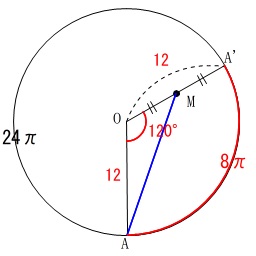
埼玉県公立高校入試18学校選択問題の数学の問題と解説

プログラミング初心者 Swift練習問題 フィボナッチ数列 Naoya Blog

福田の大学入試問題解説年版 By Jirou Fukuda

無限遠点を巡る数理 オイラー座標系 Eulerian Coordinate System 自然数 整数概念 Natural Integer Concept の再定義 Qiita

無限遠点を巡る数理 オイラー座標系 Eulerian Coordinate System 自然数 整数概念 Natural Integer Concept の再定義 Qiita

自作問題 に関する記事の一覧 Mathlog

整数問題 に関する記事の一覧 Mathlog

Uro Tekiteki 局所体に関しては森田康夫 整数論 第6章の演習問題に書いてある模様 本見ないと確信が持てなくなっている自分が悲しい Rt Jvn U 代数体の不分岐拡大はアーベル ここで見た命題でした Http T Co 3rtyaa0 局所環なら正しいのかな

中学数学 １次方程式 文章題の解き方 整数 自然数

Paypayフリマ コンプリートノート 漸化式と数学的帰納法 整数問題 東京書籍 2冊セット 解答編付き 15

大澤裕一 今の高校数学の惨状をご存じない方に簡単に説明します なぜか 統計強化が目標に 中身のない統計 箱ひげ図 四分位偏差など が必修化 一方 確率分布 期待値は選択分野 大学入試ではほぼ出題範囲外 行列 統計学などを学ぶの

算数大好き Kimagure Mana Twitter

Fx中学数学問題の解決機 By Euclidus Inc

Sat Math 数の問題 Flashcards Quizlet

中2連立方程式 計算問題 By Manabu Narawa

無限遠点を巡る数理 等差数列と等比数列 関数列 Function Sequence との関係は Qiita

整数問題 まずは整数解を求めるパターンを知ろう Youtube

方程式 1 A 1 B P 10 数学のカ

Atcoder Regular Contest 018 B 格子点と整数 思考のジャンプ幅が狭いなら 飛ぶ回数で補えばいいじゃない

倉敷芸術科学大学 入試問題について

数学まとめ Flashcards Quizlet

整数問題 に関する記事の一覧 Mathlog

ジンジンする Pdf Free Download

Telecharger 1分で左脳を鍛える算数クイズ 数学力アップで仕事がはかどる無料計算アプリ Pour Iphone Sur L App Store Jeux

勉強できるtwitterbotフォロワーまとめ Tips Of Rubbish

中学2年生数学ｰ文字式の証明 長野地区 Itto個別指導学院 長野市の学習塾

た の し い 算 数 パ ズ ル 東京工業大学デジタル創作同好会trap

東大15 整数 年号問題 大学入試 数学 過去問 Youtube

整数問題 に関する記事の一覧 Mathlog

公務員 教養 数的処理 問題集 15年版 By Agfy

中学2年生数学ｰ文字式の証明 長野地区 Itto個別指導学院 長野市の学習塾

高校数学 整数の性質をわかりやすく解説 約数の個数やユークリッドの互除法も 高校生向け受験応援メディア 受験のミカタ

自作問題4 図形と整数問題 の解答 解説 数学のカ

基本情報技術者試験午前問題集 Fequiz By Renom

Qb説明 ５年 分数のたし算 ひき算 By Suzuki Educational Software Co Ltd

来年21年を素因数分解する タイランド湾を見て暮らす パタヤコージーライフ

東大理系卒オススメ 受験生に役立つ数学動画 整数編 Okenavi

Pdf A Mixed Integer Programming Approach For Optimization Over An Efficient Set Theory And Application

Rで九九 どうして36個の数字しか使われないのか Qiita

センター数学公式 Flashcards Quizlet

ペル方程式とは 数学のカ

商品詳細ページ メディカルブックセンター

素数問題の解き方は２つしか存在しない 数学界のエース

商品詳細ページ メディカルブックセンター

本格的論述問題にチャレンジしてみよう 数学 千葉市稲毛区のハイレベル大学受験予備校 Forum 7 Oks

大学入試問題を考える Ssブログ

Popular Tweets Of 整数問題bot 1 تحليلات تويتر الرسومية الخاصة بهوتويت Whotwi

公務員 教養 数的処理 問題集 15年版 By Agfy

無限遠点を巡る数理 オイラー座標系 Eulerian Coordinate System 自然数 整数概念 Natural Integer Concept の再定義 Qiita

Fx中学数学問題の解決機 By Euclidus Inc

天体ショーを整数計画問題で解いてみた いものやま

Fx高校数学問題の解決機 アプリランキングとストアデータ App Annie

ハードウェア メモリ 数 文字の表現

マスターデーモンを解いてみたら 超短くて簡単な解答を見つけた話 流れる空の中で数学を

Qb説明 算数 ５年 分数のかけ算 わり算 By Suzuki Educational Software Co Ltd

整数問題 に関する記事の一覧 Mathlog

中学数学 連立方程式 文章題の解き方 整数 過不足問題など

カテゴリ未分類 の記事一覧 隠れ家 楽天ブログ

公務員 教養 数的処理 問題集 15年版 By Agfy

テスト記事 代入の重要性 Mathlize

小学４年生算数 けいさん ゆびドリル 計算学習アプリ App Ranking And Store Data App Annie

重複組合せの代表的な問題1 数学のカ

中３数学 整数問題の良問とその解説 難関私立高校過去問より 定期テストや高校入試に レオンの中学数学探検所

大学入試問題を考える Ssブログ

テンパズル Tenpazzle を解くツール 数学のカ

最も検索された 5 年 算数 分数 印刷とダウンロードは無料

た の し い 算 数 パ ズ ル 東京工業大学デジタル創作同好会trap